Kohärente Zustände
Der stetige Übergang von der
Mikro- zur Makromechanik,
Ergänzung zu "Harmonischer
Oszillator, quantenmechanisch"
Licht - Quanten |
Quantenoptik für Amateure
Leseproben:
Matrixoptik | Harmonischer
Oszillator | Quantisierung
des em. Feldes
Erwin Schrödinger hat in Die Naturwissenschaften 14, 664 (1926) eine in mehrfacher Hinsicht bahnbrechende Arbeit geleistet, die er selbst aber nur als ein "ganz besonders einfaches Schulbeispiel" einstufte. Sein Artikel beginnt so:
Im Jahre 1926 war es nicht ganz einfach, die Mathematik zu visualisieren. Wir untersuchen das einmal näher mit den heutigen Möglichkeiten...
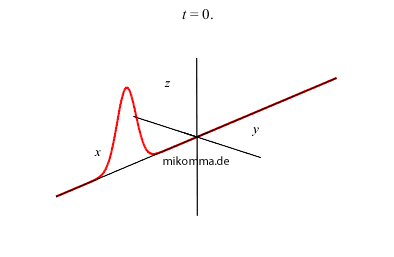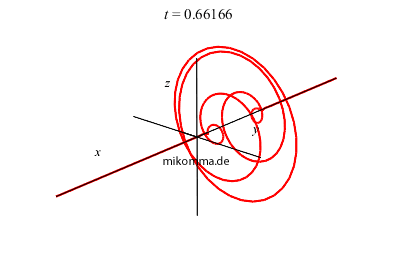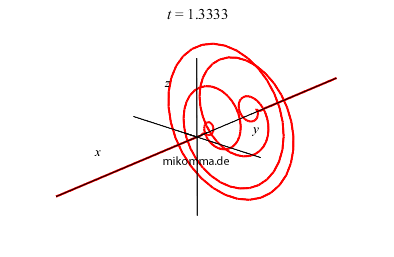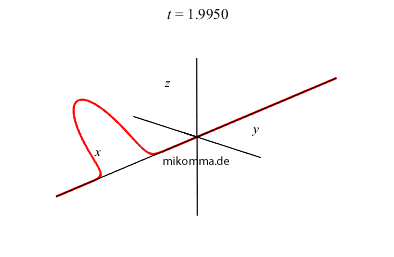 |
Summiert man die Eigenschwingungen in Gleichung (3) für n = 0 bis unendlich mit den Gewichten einer Poissonverteilung auf (siehe Harmonischer
Oszillator, quantenmechanisch), so erhält man einen geschlossenen Ausdruck für die Wellenfunktion (mithilfe der erzeugenden Funktion der Hermiteschen Polynome). Die Animation zeigt eine solche Wellenfunktion, wobei die Koordinate des Oszillators x ist, und der Realteil nach oben (z) und der Imaginärteil "nach rechts vorne" (y) abgetragen ist. Das ist zwar die "volle Wahrheit", aber nicht sehr anschaulich. Vielleicht sollten wir Schrödingers Anmerkung folgen und "wie üblich den Realteil nehmen"? |
Schrödinger: "Es mutet im ersten Moment recht bizarr an, einen Vorgang, der nach der bisherigen Auffassung der Punktmechanik angehört, durch ein System solcher Eigenschwingungen zu beschreiben. Ich möchte hier an dem gewählten einfachen Beispiel den Übergang zur makroskopischen Mechanik in concreto demonstrieren, indem ich zeige, dass eine Gruppe von Eigenschwingungen mit hoher Ordnungszahl n ("Quantenzahl") und relativ kleinen Ordnungszahldifferenzen ("Quantenzahldifferenzen") einen "Massenpunkt" darzustellen vermag, welcher die nach der gewöhnlichen Mechanik zu erwartende "Bewegung" ausführt, d. h. mit der Frequenz ν0 oszilliert."
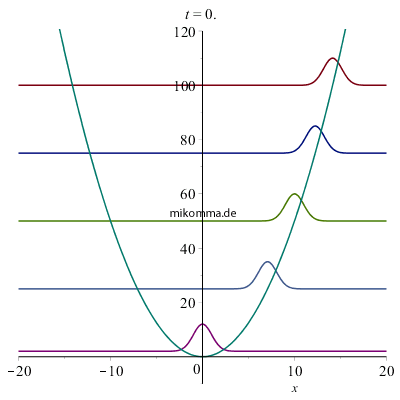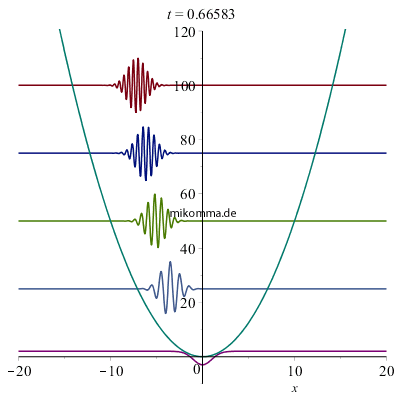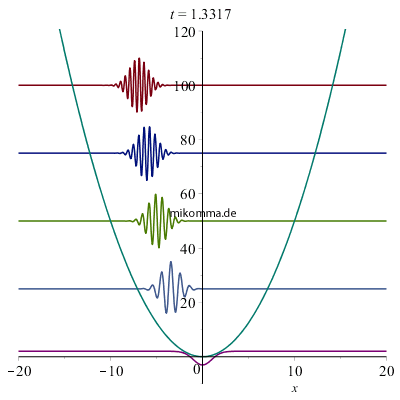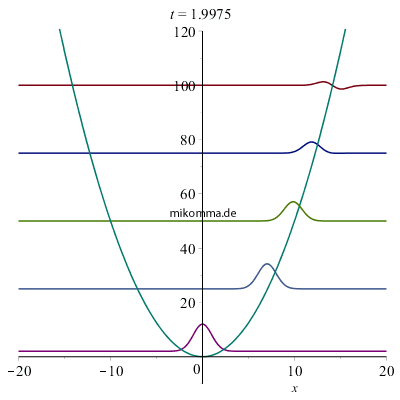 |
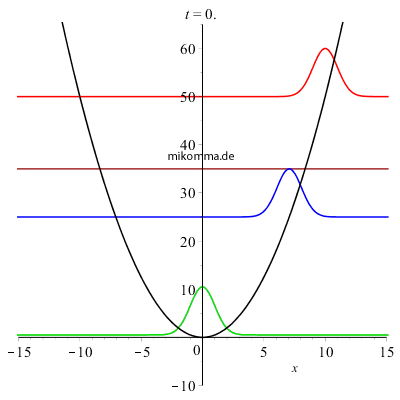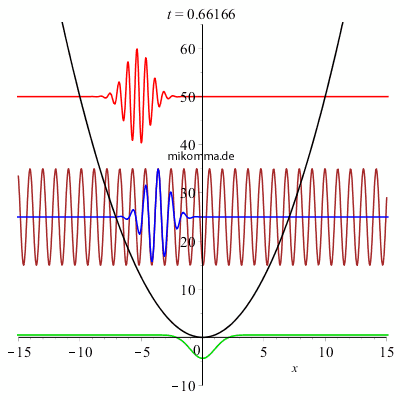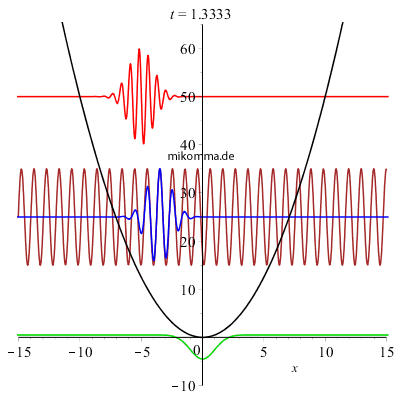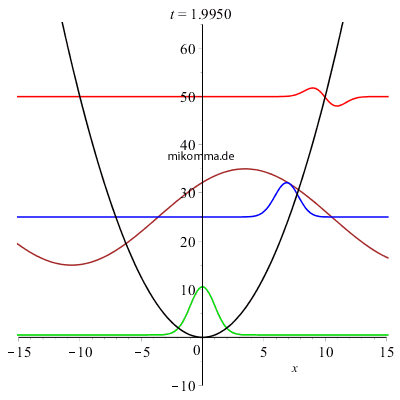
Nebenstehend sehen Sie den Realteil von Wellenpaketen im quantenmechanischen harmonischen Oszillator zu verschiedenen (frei wählbaren!) Energien oder mittleren Quantenzahlen, die hier nur zur Übersichtlichkeit äquidistant und ganzzahlig gewählt wurden. Schrödinger beschreibt das Bild so: "Ein relativ hoher und schmaler oszillierender 'Buckel' von der Gestalt einer 'GAUSSschen Fehlerkurve'... in dessen Antlitz viele tiefe und schmale Furchen gegraben sind, wodurch eine Wellengruppe entsteht... Die Anzahl und die Breite der 'Furchen' und 'Wellchen', welche den Massenpunkt durchsetzen, ist zeitlich veränderlich. Die Wellchen sind am zahlreichsten und schmälsten beim Durchgang durch die Mitte x = 0; sie werden völlig ausgeglättet an den Umkehrstellen... Die gesamte Ausdehnung der Wellengruppe ("Dicke des Massenpunktes") bleibt jedoch stets dieselbe. Die Veränderlichkeit der "Kräuselung" ist als eine Abhängigkeit von der Geschwindigkeit aufzufassen und als solche nach allgemeinen undulationsmechanischen Gesichtspunkten vollkommen verständlich - doch möchte ich an dieser Stelle hierauf nicht näher eingehen. Unsere Wellengruppe hält dauernd zusammen, breitet sich nicht im Laufe der Zeit auf ein immer größeres Gebiet aus, wie man es sonst, z. B. in der Optik, gewohnt ist." |
"Nach undulationsmechanischen
Gesichtspunkten vollkommen
verständlich": Der harmonische
Oszillator der Wellenmechanik
(oder Quantenmechanik)
beschreibt die Bewegung eines
"Massenpunktes" mithilfe von
Materiewellen. Je schneller sich
der Massenpunkt bewegt, desto
kleiner ist die ihm zugeordnete
Wellenlänge, die dann in den
Umkehrpunkten (Geschwindigkeit =
0) unendlich groß wird. Das
Paket (die Wellengruppe) bewegt
sich mit der (klassischen)
Gruppengeschwindigkeit,
zerfließt aber nicht, obwohl -
oder gerade weil? - es sich
beschleunigt bewegt. Dieses
Verhalten gibt es nur im
quadratischen Potential, also
bei einer harmonischen
Schwingung: "Unsere Wellengruppe
hält dauernd zusammen", wozu man
heute "kohärent" sagt.
Das gilt nicht nur für die von
Schrödinger in erster Linie
gemeinten großen (mittleren)
Quantenzahlen, sondern generell
(für den harmonischen Oszillator
mit Poissonverteilung). Eine
Sonderrolle nimmt dabei der
Grundzustand ein: Das
Wellenpaket (sein Betragsquadrat)
steht (schwingt nicht in
x-Richtung) und der Realteil
oszilliert mit der halben
Oszillatorfrequenz. (Die
zugehörige tiefste Kurve zur
Quantenzahl 1/2 ist künstlich
etwas nach oben verschoben, um
sie deutlicher von der x-Achse
"abzuheben". Bei ihrer
Betrachtung denke man sich einen
Draht mit "Buckel", der um seine
(horizontale) Achse rotiert.
 |
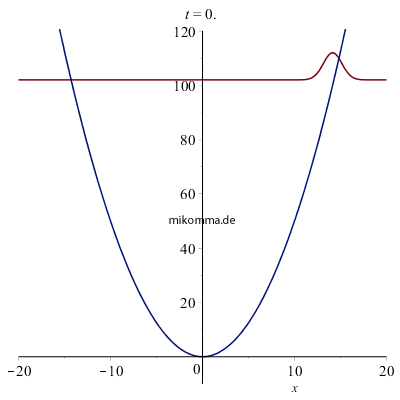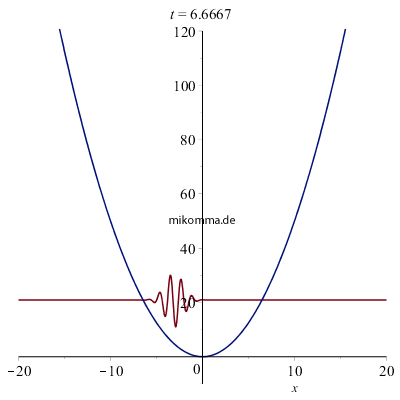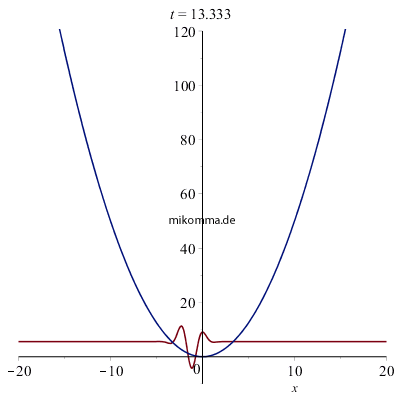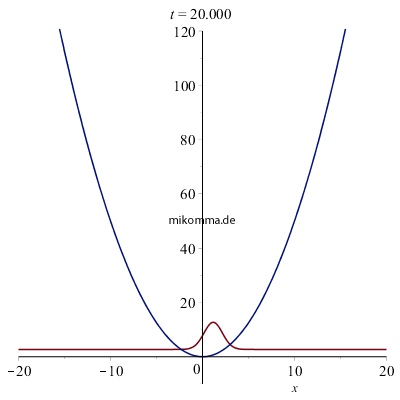
Hier ist noch eine "Lupe" zur Veranschaulichung: Oben oszilliert das Wellenpaket zur mittleren Quantenzahl 50. Darunter ist das Wellenpaket zur mittleren Quantenzahl 25 dargestellt, zusammen mit der "De Broglie-Welle" (braun), die aber nicht läuft, sondern als Ziehharmonika in Erscheinung tritt, und sich - rein rechnerisch - auch an keine Potentialgrenzen hält. Die Gauß-Einhüllende schneidet aus dieser "Ziehharmonikawelle" (mit zeitlich variierender Wellenlänge) den passenden "quaiklssischen" Teil (blau) aus. Der Grundzustand darf natürlich nicht fehlen - diesmal auf der korrekten Höhe 1/2. |
Das Wesentliche beim "Übergang von der Mikro- zur Makromechanik" ist: Makroskopische Bewegungen können aus "stationären Zuständen" der Mikromechanik (Quantenmechanik) aufgebaut werden. Die Vorstellung, dass der harmonische Oszillator in der Quantenmechanik nur diskrete Energiewerte (oder Amplituden) einnehmen kann, ist falsch.
Und Schrödinger schließt seinen Artikel mit: "Es läßt sich mit Bestimmtheit voraussehen, daß man auf ganz ähnliche Weise auch die Wellengruppen konstruieren kann, welche auf hochquantigen Keplerellipsen umlaufen und das undulationsmechanische Bild des Wasserstoffelektrons sind; nur sind da die rechentechnischen Schwierigkeiten größer als in dem hier behandelten, ganz besonders einfachen Schulbeispiel."
Also Herr Schrödinger! Ihre Bescheidenheit ("ganz besonders einfaches Schulbeispiel") in allen Ehren, aber Sie waren ein Seher! Ja, man kann auf ganz ähnliche Weise alle Vorgänge in der Atomhülle modellieren und visualisieren. Die rechentechnischen Schwierigkeiten delegieren wir heute (2015) an den Computer und ausgeklügelte Experimente bestätigen Ihre Voraussehung.
 |
Man kann mit "stationären Zuständen" sogar einen gedämpften harmonischen Oszillator beschreiben. Die undulationsmechanische Interpretation dürfte nach dem oben Gesagtem nicht schwer fallen. Was allerdings bis heute vielen orthodoxen Quantenmechanikern schwer fällt, ist das Eingeständnis, dass man dafür nur ein einzelnes (einziges) Atom braucht, siehe z.B. Quantensprung in Zeitlupe. |
Aber Schrödingers 'seminal paper' hat nicht nur den Quantensprung abgeschafft oder Experimente mit Rydbergatomen vorausgesehen, sondern auch die Grundlage für die moderne Quantenoptik geschaffen. Nach der Quantisierung des elektromagnetischen Feldes in Nummerzustände (was den stationären Zuständen des harmonischen Oszillators entspricht), hat Roy Glauber die Idee der "kohärenten Zustände" aufgegriffen und damit einen Übergang von der Teilchen- (Photonen-) zur Wellenphysik geschaffen. Der Laser lässt grüßen!
