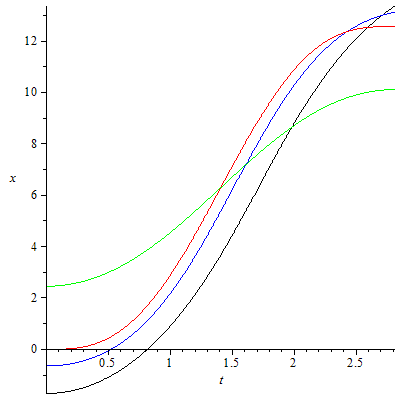
Wie kann man im Schwerefeld (konstante Kraft in eine Richtung, lineares Potential) einen Körper harmonisch (lineare Rückstellkraft, quadratisches Potential) schwingen lassen?
Das ist ohne eine Feder nicht ganz einfach und genau genommen gar nicht möglich!
Trotzdem findet man in
Generationen von Physiklehrbüchern solche Sätze
(sinngemäß):
"Wir betrachten einen harmonischen Oszillator
wie z.B. einen Ball, der reibungsfrei in einem
quadratischen Potential rollt".
Und daneben die Abbildung eines Balls auf einer
Parabel (im Schwerefeld). Besonders
in der Quantenphysik ist diese Analogie beliebt, wenn
man
den (harmonischen)
quantenmechanischen
Oszillator anschaulich beschreiben will.
Dabei weiß doch jeder Physiker, dass das Fadenpendel nicht harmonisch schwingt. Und jeder Bergsteiger ist froh, dass er leichter wird, wenn er auf den Himalaya steigt und nicht mit einem Bungee-Seil an die Talstation angebunden ist. Warum sollte also ausgerechnet eine Parabelbahn eine harmonische Schwingung zur Folge haben? Das kann wohl kaum sein: Wenn man die Parabel sehr steil macht, "schwingt" der Ball im freien Fall und das ist keine Sinusschwingung!
Also eigentlich müsste man
dieses Problem gar nicht näher untersuchen. Es
lohnt sich aber doch:
1. Theoretische Mechanik ist einfach schön!
2. Solche Märchen (zu kurz gefasste Analogien)
hindern Lernende am Verständnis, Aufklärung tut
also not!
Lassen wir also ein paar Bälle auf verschiedenen Bahnen (natürlich im homogenen Schwerefeld) "reibungsfrei rollen"!
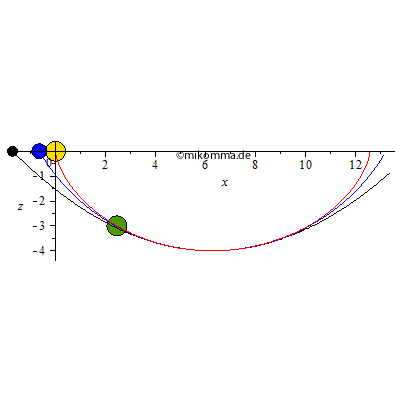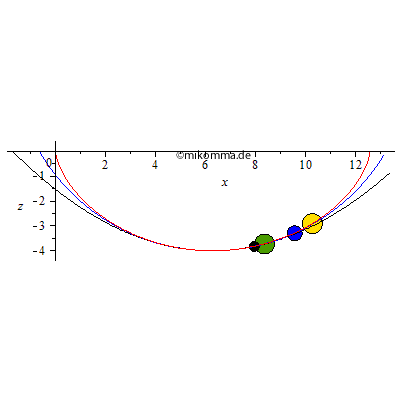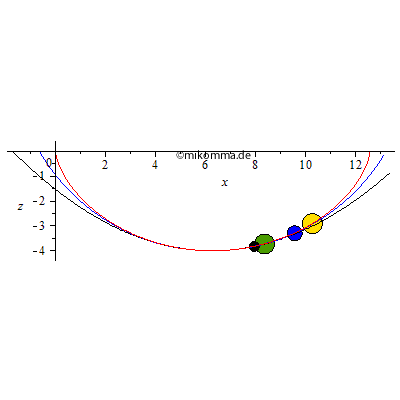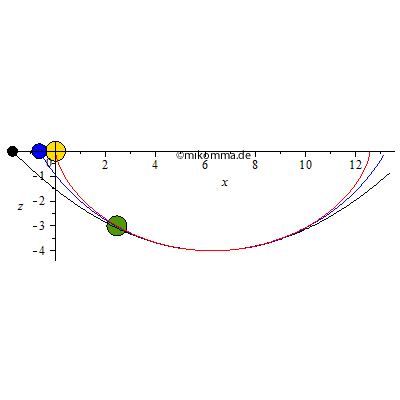
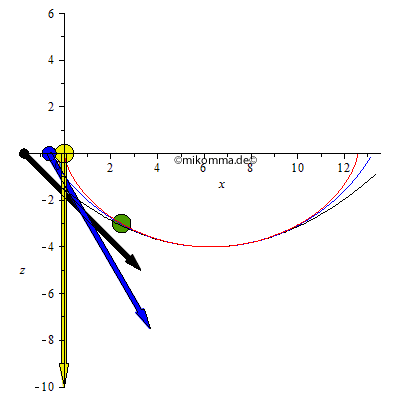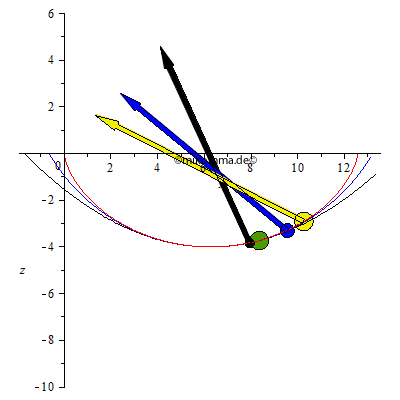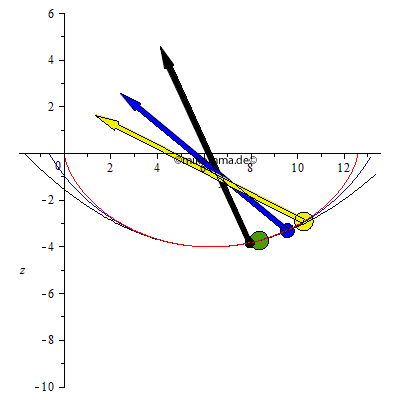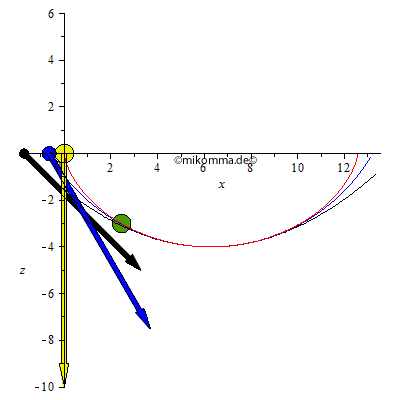
Die Bälle gleiten reibungsfrei, sie rollen nicht. Der gelbe und der grüne Ball bewegt sich auf einer Zykloidenbahn (rot, Zykloidenpendel). Der blaue auf einem Kreis (blau, Fadenpendel = Kreispendel) und der schwarze auf einer Parabel (schwarz, harmonisches Pendel??). Der grüne Ball hat die gleiche Schwingungsdauer (-> Tautochrone) wie der gelbe, nämlich die kleinstmögliche (-> Brachystochrone), wenn man den Höhenunterschied vorgibt. Alle Bahnen haben im Tiefpunkt den gleichen Krümmungsradius. Die Animation läuft nach der halben Schwingungsdauer des Zykloidenpendels rückwärts, blau und schwarz werden also "reflektiert" bevor sie den rechten Umkehrpunkt erreichen.
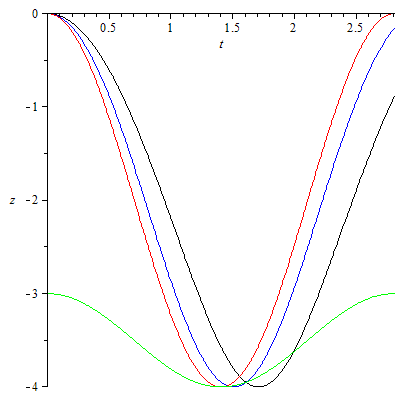
Welcher Ball schwingt nun harmonisch? Hier eine kleine Übung zum Lesen von Diagrammen (Farben siehe oben. Tipp: je höher der Grad der Ableitung, desto differenzierter die Aussage):
|
x-t-Diagramm
|
z-t-Diagramm |
vx-t-Diagramm 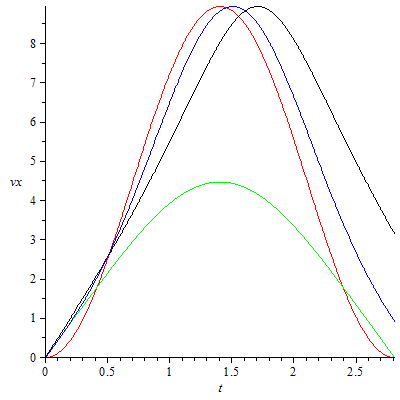
|
vz-t-Diagramm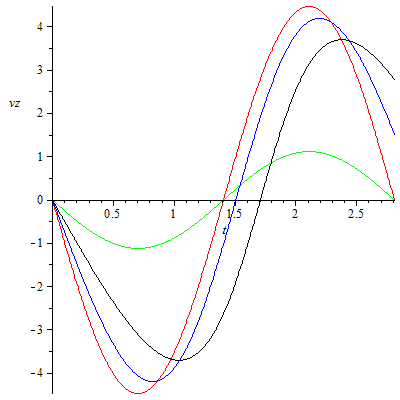 |
ax-t-Diagramm
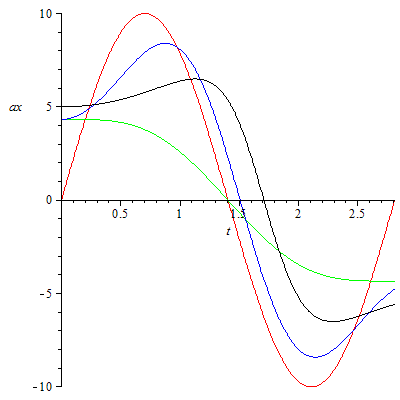
|
az-t-Diagramm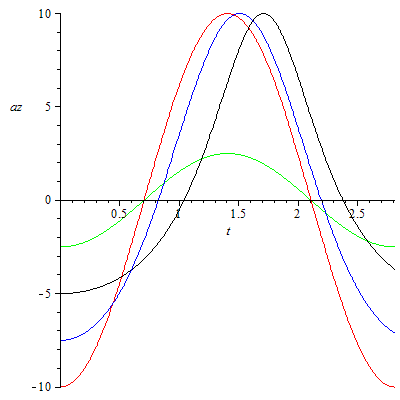
|
ax-x-Diagramm
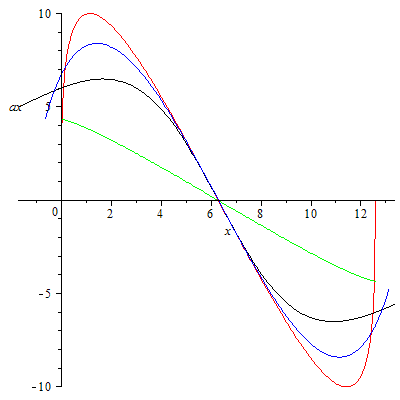
|
az-z-Diagramm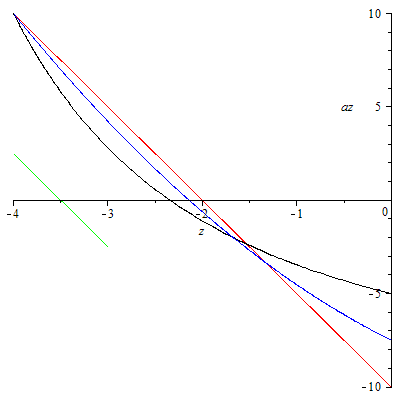
|
Und die Moral von der Geschicht? Das gute alte Fadenpendel ist für kleine Auslenkungen die beste Analogie für harmonische Schwingungen im Schwerefeld. Aber das wussten wir ja schon immer!
Oder haben
wir etwas
vergessen? Was
sagen uns diese
Animationen?
|
Evolution!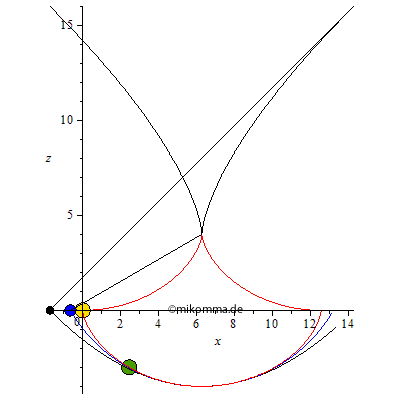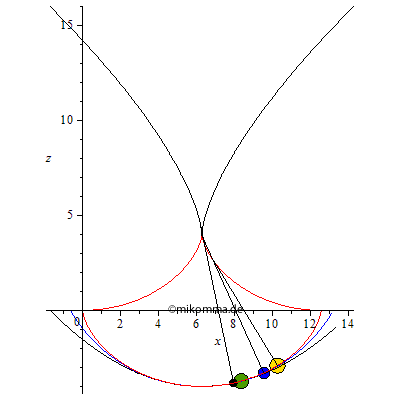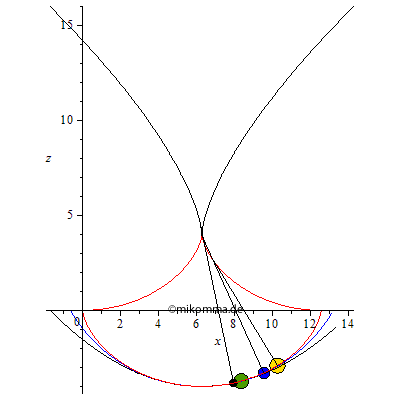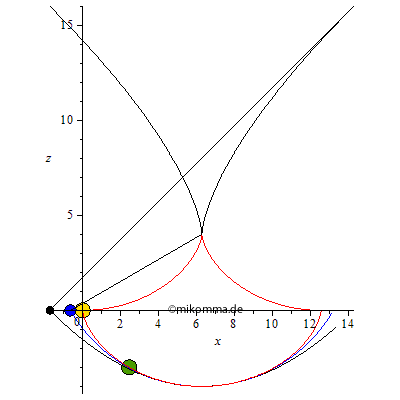
|
Also könnte man die Schwingung doch auch dadurch harmonisch machen, dass die anharmonischen Pendel an der passenden Stelle "reflektiert" werden? Und wie würde dann das quantenoptische Analogon aussehen?
Etwas ernsthafter: In der linken Animation oben sind die resultierenden Beschleunigungen dargestellt, in der rechten die Evoluten (falls jemand ein Zykloidenpendel und "Parabelpendel" konstruieren will).
Wenn man so will, schwingt das Zykloidenpendel also harmonisch, weil der Massenpunkt zu jeder Zeit die (betragsmäßig) gleiche "Zentripetalbeschleunigung" erfährt. Allerdings bewegt sich das Kreiszentrum (gleichförmig in x-Richtung), so dass nur die Schwingung in z-Richtung streng harmonisch ist. Man beachte auch die Beschleunigungsdiagramme weiter oben, insbesondere das ax-x-Diagramm. Im ax-t-Diagramm ist für das Zykloidenpendel zwar ein Sinus zu sehen (und es ist wirklich einer), aber auch das gilt nur für das gelbe Zykloidenpendel. Hier lauert übrigens ein weiterer Trugschluss: Wenn man die Zykloidengleichung in Parameterform zwei Mal nach dem Parameter ableitet, erhält man die Parameterdarstellung eines Kreises. Also eine harmonische Schwingung? Nicht unbedingt! Es gibt beliebig viele Parameterdarstellungen einer mathematischen Kurve, aber die physikalische Bewegung läuft in der einen Zeit ab (wenn sie nicht zu schnell abläuft :-).
Dass der Versuch, ein harmonisches Pendel im Schwerefeld (und ohne Feder) zu betreiben, das mit beliebigen Frequenzen und Auslenkungen funktioniert, zum Scheitern verurteilt ist, zeigt auch die Animation mit den Evoluten: Um die Anharmonizität des Kreispendels zu kompensieren, muss die Fadenlänge laufend verkürzt werden (im Vergleich zum Kreispendel). Mit einer laufenden Verlängerung des Fadens wie etwa beim Parabelpendel wird die Schwingung nur noch anharmonischer. Das Zykloidenpendel markiert also ein "relatives Optimum". Relativ in diesem Sinne: Die Zykloidenkurve hat in den Umkehrpunkten eine senkrechte Tangente, hier wirkt also die volle Fallbeschleunigung. Aber mehr ist nun einmal aus dem Schwerefeld nicht herauszuholen. Wer also mit Hilfe einer "geeigneten Bahn" aus dem Schwerefeld das Feld einer Feder machen will, muss wissen, dass diese "Feder" ab einer gewissen Dehnung nur noch eine konstante Kraft liefert.
Wussten wir das nicht schon immer?
© M. Komma 01/2011
Methode: Aufstellen der Differentialgleichungen mit Lagrange (wahlweise 1. oder 2. Art) und Maple. Lösung der Differentialgleichungen mit Maple, z.B. mit " Newtons Maschine". Die Differentialgleichung für die Zykloide lässt sich geschlossen lösen.
Siehe auch:
Kreispendel
Zykloidenpendel
Harmonischer Oszillator, quantenmechanisch
Schrödingers Oszillator
Paulfalle, Standard
Paulfalle, Mechanisches Analogon | Paulfalle, Mechanisches Analogon, Details