
Das Foucaultsche Pendel
Ein paar Anmerkungen zum Thema
"Das sphärische Pendel im rotierenden Koordinatensystem"

|
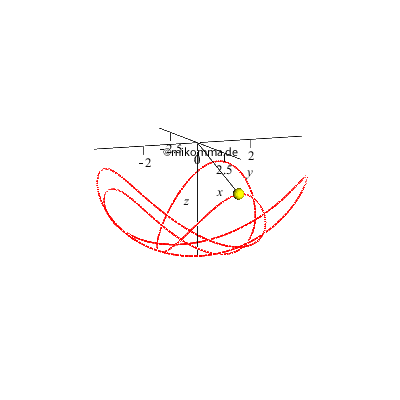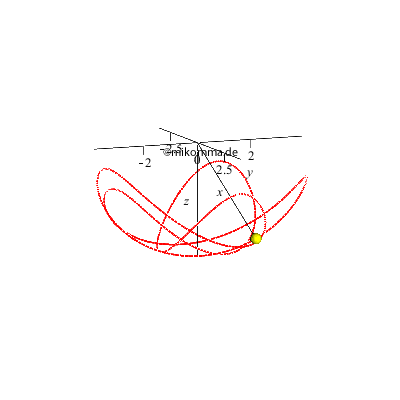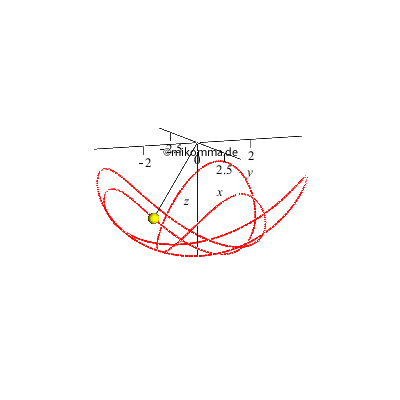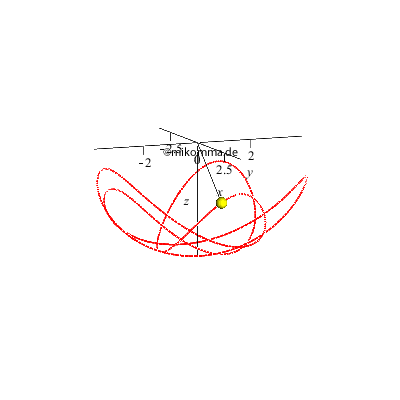
Vorbemerkung Die Bewegungsgleichungen des sphärischen Pendels im Inertialsystem lauten in Kugelkoordinaten (Polarwinkel θ = 0 am "Nordpol" (z>0), Azimut Φ, Radius r=R=Pendellänge):
Wie beim ebenen Kreispendel gibt es natürlich auch hier nur numerische Lösungen, weil die Schwingung eines jeden Schwerependels genau genommen nicht harmonisch ist. Dieser kleine aber wichtige Unterschied (der Anharmonizität) führt z.B. dazu, dass ein Schwerependel nie exakt auf einer stationären Ellipse schwingt, sondern dass die Ellipse präzediert, und zwar in dem Sinn, in dem sie vom Pendelkörper durchlaufen wird. Das ebene Pendel (Ellipse mit einer Halbachse = 0), das seine Schwingungsebene beibehält, ist also eine Idealisierung. Die nächste Animation zeigt die Projektion der 3D-Darstellung von oben auf die horizontale (x-y-) Ebene (eine geschlossene Bahn ist nur ein Sonderfall):
Man kann dieses Verhalten des Schwerependels mit einer Abwandlung des Flächensatzes (Bewegung im Zentralfeld) begründen: Der Azimut kann sich nur in eine Richtung ändern (ohne äußere Kraft/Störung), also nicht zunehmen und dann wieder abnehmen, wie z.B. beim Lissajous-Pendel (s.u.). Diese "intrinsische Präzession" lässt sich im allgemeinen Fall nicht mit einem geschlossenen Ausdruck angeben, sondern nur durch numerische Berechnung der zugehörigen elliptischen Integrale (siehe Mathematisches Pendel). Für "kleine Auslenkungen" kann man aber eine gute Näherung verwenden, siehe z.B. J.L. Synge and B.A. Griffith "Principles of Mechanics", S. 381. Danach präzediert die Schwingungsellipse in einer Schwingung azimutal um den Winkel (betragsmäßig, im Bogenmaß) Δφ = 3A/4R2 , wobei R die Pendellänge und A die Fläche der Ellipse ist. Das Vorzeichen dieses "Flächeneffekts" hängt davon ab, in welchem Drehsinn die Ellipse durchlaufen wird, kann also den "Foulcaulteffekt" (Rechtsablenkung auf der Nordhalbkugel) schwächen oder verstärken. Nachdem die große Halbachse durch die Auslenkung des Pendels vorgegeben wird, kommt es also darauf an, die kleine Halbachse klein zu halten. Ein auf der Erde ausgelenktes und dann losgelassenes Pendel startet im Inertialsystem aber immer mit der "Winkelgeschwindigkeit der Erde" (senkrechte vom Breitengrad abhängige Komponente), bzw. es dürfte nicht ganz einfach sein, es so loszulassen, dass diese azimutale Anfangsgeschwindigkeit genau kompensiert wird. Nach dieser Vorbemerkung nun zum Thema "Das sphärische Pendel im rotierenden Koordinatensystem": Foucaultsches Pendel Da die Erde sehr langsam rotiert (senkrechte Komponente der Winkelgeschwindigkeit bei 48° Breite: Ω = 0,000054Hz), arbeiten wir zunächst mit einem Modell. a) Modell: Ein Pendel der Länge R =
10cm schwingt mit der Kreisfrequenz ω =
10Hz (g = 10m/s2). Es wird um 5cm ausgelenkt und dann
losgelassen. Welche Bahn würde es beschreiben, wenn die
Erde mit Ω = 0,5Hz rotieren würde? Im Hinterkopf hat man etwa diese "Bahn eines Foucaultschen Pendels" (Projektion auf die horizontale Ebene):
Das Pendel startet im rotierenden System (auf der Erde) aus der Ruhelage (rechts bei x = 0.05) und wird auf der Nordhalbkugel durch die Corioliskraft nach rechts abgelenkt (wie die Luft, die in ein Tiefdruckgebiet strömt). Das Pendel schwingt also nicht durch den Ursprung (x=y=0), sondern rechts daran vorbei. Auf dem Rückweg wiederholt sich das, und deshalb dreht sich die "Schwingungsebene" des Pendels nach rechts. Das ist im Prinzip auch richtig, aber wie passt das zur "Linksdrehung" der Ellipsen im Inertialsystem? Im Inertialsystem (wenn die Erde nicht rotieren würde, bzw. am Äquator, aber das Pendel mit der azimutalen Winkelgeschwindigkeit 0,5Hz startet) sieht die Bahn des Pendels so aus:
Die Schwingungsellipse dreht sich also nach links. Und wenn wir schon dabei sind, die Rotationsgeschwindigkeit der Erde frei zu wählen, können wir auch ihr Vorzeichen ändern und Ω von -0,5Hz bis 0,5Hz laufen lassen (was einer Wanderung von Australien nach Europa entspricht :):
Alles klar? Übrigens: die oben dargestellten Bahnen wurden für acht Schwingungen mit der Schwingungsdauer eines harmonischen Pendels berechnet. Woran sieht man das? Und wie sieht nun die Bahn eines "realen Foucault-Pendels" aus? b) Realistisches Zahlenbeispiel: Pendellänge R = 3m, Auslenkung in x-Richtung 1m. In der folgenden Animation startet das Pendel im Inertialsystem immer mit der azimutalen Winkelgeschwindigkeit der Erde (bei 48°), die Winkelgeschwindigkeit Ω des rotierenden Koordinatensystems (des gedachten Beobachters) wird aber von 0 bis zum realen Wert der Erdrotation verändert (laufende Zahlenwerte oben):
Wenn man die unterschiedliche Skalierung der Achsen (MKS-Einheiten) beachtet, kann man der Animation entnehmen wie weit sich die Schwingungsebene des Pendels im Inertialsystem und auf der Erde in fünf Schwingungen dreht. Dabei stellt man fest, dass die im Inertialsystem "rückwärts drehende Ellipse" im Vergleich zur Corioliskraft nur einen geringen Effekt hat. Mit anderen Worten: Wenn ein Foucault-Pendel "rückwärts dreht" (z.B. im Schulversuch), dann liegt das i.A. nicht an den Anfangsbedingungen ("schlechter Start"), sondern an Störungen, die sich im Laufe der Zeit aufsummieren (oder aufschaukeln) können. Lissajous-Pendel Die "intrinsische Präzession" des sphärischen
Pendels wird manchmal so erklärt, bzw.
"verständlich gemacht": Wie sehen die Bahnen eines Lissajous-Pendels aus? Zur Illustration eine weitere Animation:
Zur besseren Übersicht sind die unterschiedlich langen Achsen der Ellipsen gleich lang dargestellt, man denke sich also die kleine Halbachse (y) um fünf Größenordnungen kleiner, wenn man die Wirkung des "Flächeneffekts" quantitativ beurteilen will. Der Parameter d der Animation ist die prozentuale Abweichung der Frequenz der azimutalen (schnelleren) Schwingung von der radialen (langsameren) Schwingung. Man sieht: Lissajous-Pendel haben keine intrinsische Präzession! Der Azimut kann zu- und wieder abnehmen. Und: Im Laufe der Zeit füllt die Bahn eines Lissajous-Pendels ein Rechteck aus, während die Bahn eines sphärischen Pendels die Fläche zwischen den Apsidenkreisen ausfüllt (geschlossene Bahnen ausgenommen). "Tiefere Ursache": Im Gegensatz zum (idealen) Lissajous-Pendel ist das sphärische Pendel nicht nur anharmonisch, sondern auch anders aufgehängt. Das Lissajous-Pendel hat die Freiheitsgrade x und y (bewegt sich in der x-y-Ebene), das sphärische Pendel die Freiheitsgrade Θ und φ (bewegt sich auf einer Kugel). Man sollte also Kugelkoordinaten nicht einfach durch rechtwinklige ersetzen - auch nicht für kleine Amplituden...
|
© M. Komma 05/2018
Methode: Numerische Lösung der Differentialgleichungen mit Maple, siehe
auch "Newtons
Maschine".
Siehe auch:
Kugelpendel
Kugelpendel, Details
Kreispendel
Überschlag
Mathematisches Pendel
Zykloidenpendel
Das Märchen vom harmonischen Oszillator im Schwerefeld
Harmonischer Oszillator,
quantenmechanisch
Paulfalle, Standard
Paulfalle, Mechanisches Analogon |
Paulfalle, Mechanisches Analogon,
Details
HOME | Projekte | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top