Kugelpendel (sphärisches Pendel), Details 

Auszüge aus einem Maple-Worksheet 

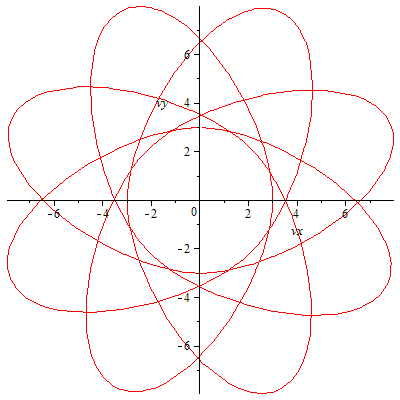
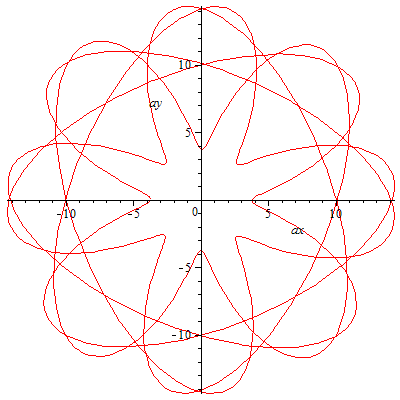
Wir betrachten wieder den Sonderfall einer geschlossenen Bahn, der nur dann eintritt, wenn die Anfangsbedingungen passend gewählt sind (was nur numerisch berechnet werden kann -> elliptische Integrale).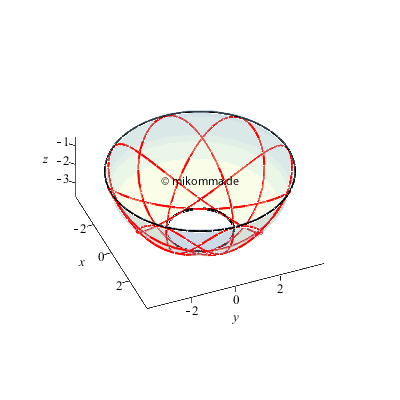 

Das Pendel bewegt sich zwischen zwei Breitenkreisen (schwarz), die durch die Energie- und Drehimpulserhaltung vorgegeben sind. Im "Normalfall" der nicht geschlossenen Bahn wird jeder Punkt zwischen diesen Breitenkreisen irgendwann einmal erreicht (vgl. Lissajous-Figuren).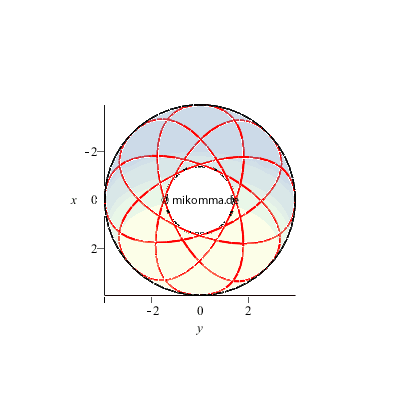 

Die Einzelheiten der Bewegung lassen sich an folgenden Diagrammen ablesen. 

Kugelkoordinaten 

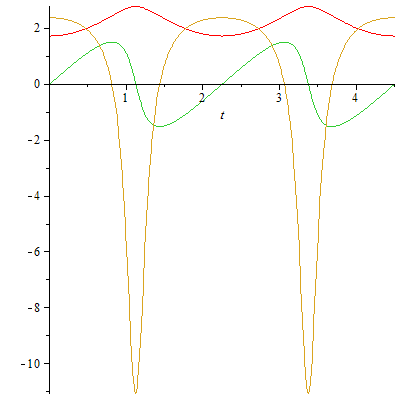
Polarwinkel (rot), Winkelgeschwindigkeit (grün) und Winkelbeschleunigung (goldbraun) als Funktion der Zeit. 

>	plot([tht(t),omtht(t),ath(t)],t=0..4.5);

 

Achtung: Der Polarwinkel wird von oben (Nordpol) gemessen, die Maxima der roten Kurve gehören also zur tiefsten Lage (unterer Breitenkreis) des Pendels. Dass die polare Winkelgeschwindigkeit dort Null wird, bedeutet nicht, dass das Pendel stillsteht; vielmehr macht in dieser Lage eine reine Drehbewegung um die senkrechte Achse:

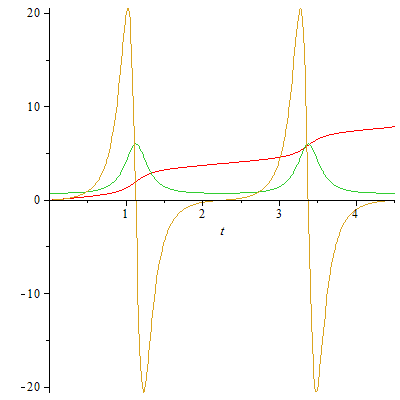
 Azimut 

>	plot([pht(t),omt(t),aph(t)],t=0..4.5);

 

Nach einer vollen "polaren Periode" (die höchste Lage wird zum zweiten Mal wieder erreicht), ist die azimutale Präzession 1/4 Umdrehung. Die azimutale Winkelgeschwindigkeit muss wegen der Drehimpulserhaltung zunehmen, wenn sich das Pendel der vertikalen Drehachse nähert und wieder abnehmen, wenn es sich entfernt. 

Kartesische Koordinaten 

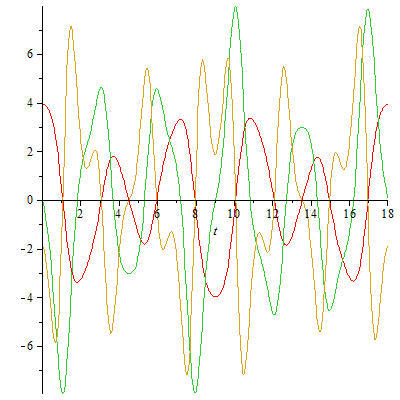
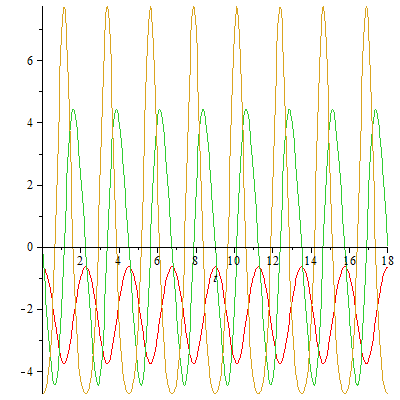
x-Koordinate, Geschwindigkeit und Beschleunigung in x-Richtung 

>	plot([x,vx,ax/2],t=0..18);

 

Die Diagramme sind nun etwas komplexer, dafür sieht man die volle Periode der geschlossenen Bahn besser. 

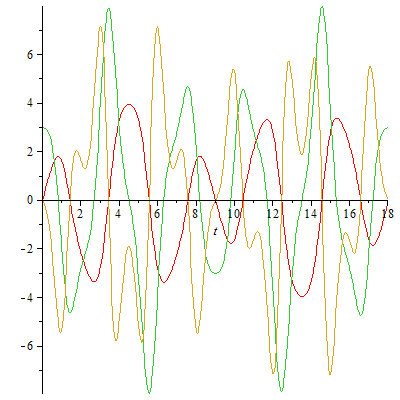
Bewegung in y-Richtung: 

>	plot([y,vy,ay/2],t=0..18);

 

Am einfachsten sind die Verhältnisse bei der Bewegung in z-Richtung: fast harmonisch. 

>	plot([z,vz,az/2],t=0..18);

 

Weitere Phasendiagramme (v steht für Geschwindigkeit, a für Beschleunigung): 

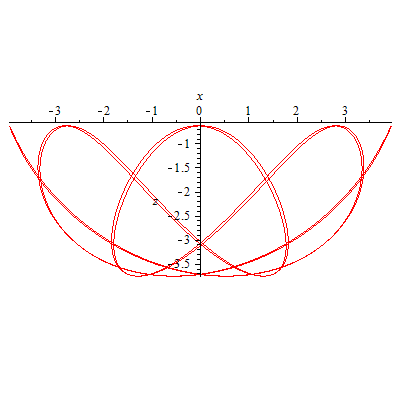
>	plot([x,z,t=0..18],labels=['x','z'],scaling=constrained);

 

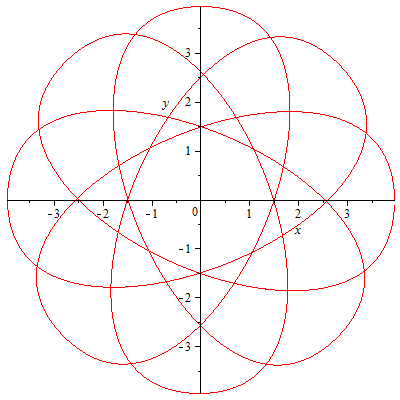
>	plot([x,y,t=0..18],labels=['x','y'],scaling=constrained);

 

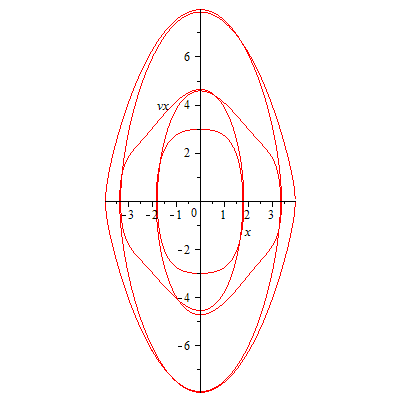
>	plot([x,vx,t=0..18],labels=['x','vx'],scaling=constrained);

 

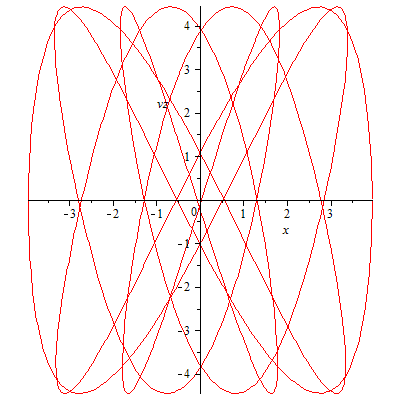
>	plot([x,vz,t=0..18],labels=['x','vz'],scaling=constrained);

 

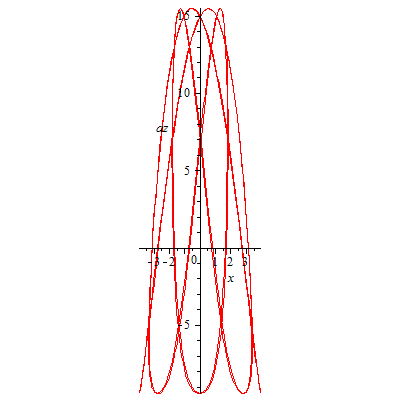
>	plot([x,az,t=0..18],labels=['x','az'],scaling=constrained);

 

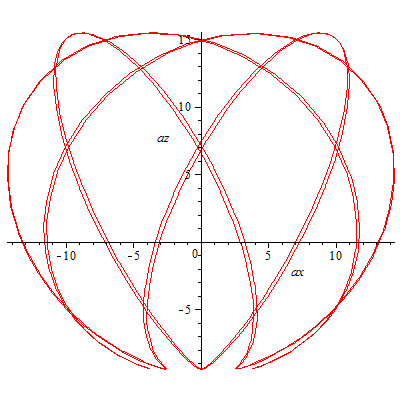
>	plot([ax,az,t=0..18],labels=['ax','az'],scaling=constrained);

 

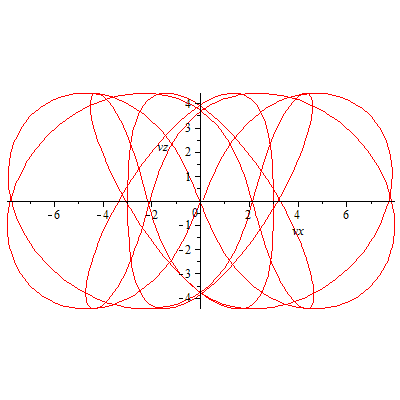
>	plot([vx,vz,t=0..18],labels=['vx','vz'],scaling=constrained);

 

>	plot([vx,vy,t=0..18],labels=['vx','vy'],scaling=constrained);

 

>	plot([ax,ay,t=0..18],labels=['ax','ay'],scaling=constrained);

 

© M. Komma 02/2011
Für die html-Ausgabe von Maple bin ich nicht verantwortlich...

Methode: Numerische Lösung der Differentialgleichungen mit Maple, siehe auch "Newtons Maschine".

Siehe auch:
Kugelpendel
Kreispendel
Überschlag
Mathematisches Pendel
Zykloidenpendel
Das Märchen vom harmonischen Oszillator im Schwerefeld
Harmonischer Oszillator, quantenmechanisch
Paulfalle, Standard
Paulfalle, Mechanisches Analogon | Paulfalle, Mechanisches Analogon, Details

Moderne Physik mit Maple